Two-Dimensional Gabor Filters

 
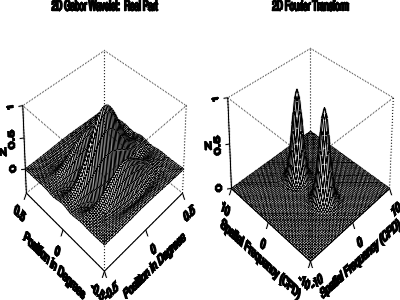
Figure 2: The real part of a 2-D Gabor wavelet, and its 2-D Fourier transform. From Daugman (1980) [8].

An effective strategy for extracting both coherent and incoherent textural information from images, such as the detailed texture of an iris, is the computation of 2-D Gabor phasor coefficients. This family of 2-D filters were originally proposed in 1980 by Daugman [8] as a framework for understanding the orientation-selective and spatial-frequency-selective receptive field properties of neurons in the brain's visual cortex, and as useful operators for practical image analysis problems. Their mathematical properties were further elaborated by the author in 1985 [9], who pointed out that these 2-D quadrature phasor filters were conjointly optimal in providing the maximum possible resolution both for information about the orientation and spatial frequency content of local image structure (in a sense ``what"), simultaneously with information about 2-D position (in a sense ``where"). The complex-valued family of 2-D Gabor filters uniquely achieves the theoretical lower bound for conjoint uncertainty over these four variables, as dictated by an inescapable uncertainty principle [9].

These properties are particularly useful for texture analysis [2], [4]-[7], [10], [14]-[16], [18], [23], [29]-[31] because of the 2-D spectral specificity of texture as well as its variation with 2-D spatial position. A rapid method for obtaining the required coefficients on these elementary functions for the purpose of representing any image completely by its 2-D Gabor Transform, despite the non-orthogonality of the expansion basis, was given in [10] through the use of a relaxation neural network. A large and growing literature now exists on the efficient use of this non-orthogonal expansion basis and its applications (e.g. [2],[14],[23],[28]).

Two-dimensional Gabor filters over the image domain (x,y) have the functional form

where (x_o,y_o) specify position in the image, (,,) specify effective width and length, and (u_o,v_o) specify modulation, which has spatial frequency _o = (u_o² + v_o²) ^½ and direction _o = arctan( v_o/u_o). (A further degree-of-freedom included below but not captured above in (5) is the relative orientation of the elliptic Gaussian envelope, which creates cross-terms in xy.) The 2-D Fourier transform F(u,v) of a 2-D Gabor filter has exactly the same functional form, with parameters just interchanged or inverted [9]:

The real part of one member of the 2-D Gabor filter family, centered at the origin (x_o,y_o) = (0,0)and with aspect ratio (/) = 1 is shown in Figure 2, together with its 2-D Fourier transform F(u,v).

2-D Gabor functions can form a complete self-similar 2-D wavelet expansion basis [10], with the requirements of orthogonality and strictly compact support [20]-[21] relaxed, by appropriate parameterization for dilation, rotation, and translation. If we take (x,y) to be a chosen generic 2-D Gabor wavelet, then we can generate from this member a complete self-similar family of 2-D wavelets through the generating function

where the substituted variables (x',y') incorporate dilations of the wavelet in size by 2 to the power -2m, translations in position (p,q), and rotations through angle Ø:

It is noteworthy [9] that as consequences of the similarity theorem, shift theorem, and modulation theorem of 2-D Fourier analysis, together with the rotation isomorphism of the 2-D Fourier transform, all of these effects of the generating function (7) applied to a 2-D Gabor mother wavelet (x,y) =G(x,y)in order to generate a 2-D Gabor daughter wavelet _mpqØ have corresponding or reciprocal effects on its 2-D Fourier transform F(u,v) without any change in functional form. This family of 2-D wavelet filters and their 2-D Fourier transforms is closed under the transformation group of dilations, translations, and rotations [9]. We will exploit these self-similarity properties of 2-D Gabor filters in analyzing iris textures across multiple scales to construct identifying codes.