Number of Independent Degrees-of-Freedom in an Iris Code

Although there are 256 bytes or 2,048 bits in any given iris code, such a code possesses far fewer than 2,048 independent binary degrees-of-freedom. One reason is that there are substantial radial correlations within an iris. For example, a given furrow or ciliary process tends to propagate across a significant radial distance in the iris, exerting its influence on several remote parts of the code, thus reducing their independence. Similarly, a feature such as a furrow influences different parts of the code associated with several different scales of analysis, since the Fourier spectrum of such a punctate feature can span several octaves. Finally, inherent correlations are introduced by the bandpass property of the 2-D Gabor filters, specifically by the finite bandwidth determined by parameters , , and in (13).

As pointed out by Norbert Wiener [32], any signal convolved with a linear filter acquires a correlation distance that is greater than or equal to the reciprocal of the bandwidth of the filter. This property is well-known for lowpass filters but is perhaps less widely recognized for bandpass filters. Even though the peak response of the bandpass filter might be at a very high frequency, its passband introduces phase coherence that lingers for a greater number of cycles, the narrower its bandwidth. (This is easily grasped by considering the limiting case of the coherent response generated by a notch-pass filter.) In the present case the correlations introduced inherently by the bandlimited 2-D Gabor filters alone reduce the information capacity of the iris code by a factor of 4.05, from 2,048 bits to about 506 bits, given the values of , , and the sampling densities employed at the different scales of analysis.

The number of independent degrees-of-freedom typically remaining in an iris code after both of these sources of correlation have been factored in (those arising from the 2-D Gabor filters and those inherent within an iris), can be estimated by examining the distribution of Hamming distances computed across a population of unrelated iris codes. Comparing each pair of iris codes A and B bit-by-bit, their normalized Hamming distance HD is defined here as the fraction of disagreeing bits between them:

where the Boolean operator (XOR) equals 1 if and only if the two bits A_j and B_j are different.

Since each bit of any iris code has equal a priori odds of being a 1 or a 0, there is probability p=0.5 that any pair of bits from different iris codes disagree. (Each of the four states 00, 01, 10, 11 has probability 0.25; the bits agree in two cases and disagree in the other two.) If each of the 2,048 bits in a given iris code were fully independent of every other bit, then the expected distribution of observed Hamming distances between two independent such iris codes would be a binomial distribution with p=0.5 and N=2,048 (in other words, equivalent to tossing a fair coin 2,048 times, and counting the fraction of heads in each round of 2,048 tosses). Once the intrinsic code correlations introduced by the 2-D Gabor filters were factored in, the distribution should be a binomial with p=0.5 and N=506 if the iris itself had no inherent correlations.

 
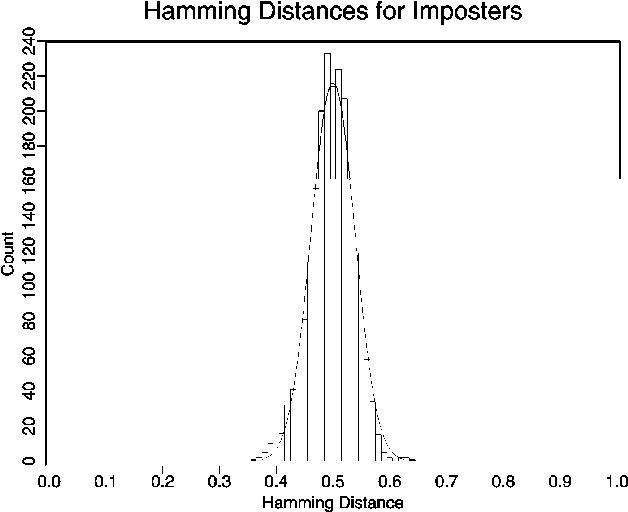
Figure 6: Distribution of Hamming distances between unrelated iris codes. Solid curve is Eqt. (22). Compare this to the improved performance in the BT evaluation

The actual distribution of observed Hamming distances between codes for different irises is shown in Figure 6, which is generated from 2,064 complete comparisons between unrelated pairs of iris codes. This empirical distribution has a standard deviation of = 0.038, with a mean of µ = 0.497. Since the standard deviation of a binomial distribution is given by = (pq/N)^½ (where q=1-p), this distribution of Hamming distances would correspond to a binomial process with N=173 Bernoulli trials per run. Given the estimate of roughly a four-sample correlation distance introduced by the 2-D Gabor encoders, we can now estimate that a bound on the ``source entropy," reflecting the number of degrees-of-freedom of variation typical of iris texture resolved to 2,048 samples, would be something like 690 bits.

The binomial distribution for N Bernoulli trials with outcome probabilities p and q predicts that the likelihood of observing a fraction x=m/N events among the N trials is:

A theoretical plot of the probability density function associated with such a binomial process having N=173 and p=0.5 is also shown in Figure 6 as a smooth curve, and it offers a good fit to the data. In summary it appears that there exist the equivalent of about 173 independent binary degrees-of-freedom typically remaining in a 2,048-bit iris code, once both the correlations introduced by the 2-D Gabor filters and those inherent in the iris have been factored in. The likelihood of two iris codes from different irises agreeing completely by chance is thus roughly one in 2¹⁷³, or approximately 10^-52.